整数の加法の定義

ここでは、整数の加法を定義していきます。

ここまでの整数についての振り返り

整数の定義 や 自然数の整数への埋め込み の冒頭でも見ましたが、まずは簡単に整数についておさらいしておきます。

自然数 $a,b$ を使って、自然数のペア $(a,b)$ を考えます。このとき $[(a,b)]$ を次のように定義してグループ分けをしていきます。

これは、整数を $a-b$ で表そうというアイデアに基づいています。 $a+d=c+b$ なら $a-b=c-d$ が成り立つのだから、同じ整数を表すと考えて、同じグループに属するようにしています。こうして作られる $\lbrace [(a,b)] \rbrace$ を整数の集合といい、各元を整数と呼ぶのでした。

例えば、 $(1,3)$ や $(2,4)$ や $(10000,10002)$ はいずれも同じグループ $[(1,3)]$ に属していて、このグループは $-2$ を表していると考える、というわけです。

整数の加法はどう定義するのが自然か？

このように整数を定義した場合、整数の加法はどう定義するのが自然でしょうか。

2つの整数を、 $[(a,b)]$ と $[(c,d)]$ としましょう（ $a,b,c,d$ は自然数）。これらは、心の中では $a-b$ と $c-d$ を表している、と考えます（が、本シリーズではまだ引き算を定義してないので、表舞台には出しません）。

こうしたとき、高校までの整数の足し算を思い出せば、この2つの和は\[ (a-b)+(c-d)=a-b+c-d \]とするのが自然です。が、再びですが、引き算はまだ定義していないので、この書き方はまずいです。しかし、右辺を\[ (a+c)-(b+d) \]とすればどうでしょうか。これは、すでに定義した書き方を使えば、 $[(a+c,b+d)]$ と表すことができます。

以上のことから、2つの整数 $[(a,b)]$ と $[(c,d)]$ の和は、 $[(a+c,b+d)]$ になる、と定義するのが自然です。これを整数の加法と定義すると、今までに扱ってきた整数の加法と整合的になる、と考えられます。

「代表元によらない」について

「整数の加法はこのように定義するのが自然だ」という話を書きましたが、実はちょっと問題があります。

というのも、整数は2つの自然数を使って $[(a,b)]$ と表すのですが、この表し方は1通りではないからです。なので、 $[(a,b)]$ と $[(c,d)]$ の和を\[ [(a+c,b+d)] \]と定義するのが自然だとしても、 $[(a,b)]$ を別の表し方にしたときに、結果が変わってしまうかもしれません。こんなことが起こると、困ってしまいます。そのため、「こんなことは起こらないよ」というチェックが必要です。

もっと具体的に、「困ったこと」とはどういうことなのか、見てみましょう。例えば、2つの整数 $[(a,b)]$, $[(c,d)]$ の積を\[ [(ac,bd)] \]で定義したとしましょう（後のページで導入する積とは違うものです）。実は、このように定義すると、定義が破綻してしまいます。

例えば、 $-2$ と $-3$ を、 $[(1,3)]$, $[(2,5)]$ と表したとしましょう。先ほどの定義に従えば、この積は\[ [(1\cdot 2, 3\cdot 5)]=[(2, 15)] \]となります。 $-2$ を表す方法は他にもあって、 $[(10,12)]$ とすることもできます。こうすると、先ほどの定義に従えば、積は\[ [(10\cdot 2, 12\cdot 5)]=[(20, 60)] \]となります。この2つの結果 $[(2,15)]$ と $[(20,60)]$ を見比べると、前者は $-13$ で、後者は $-40$ に対応しており、別の整数を表していることがわかります。

つまり、整数は、表し方が複数ある（自然数のペアの選び方が複数ある）ので、どのペアを選ぶかによって、答えが変わってしまうかもしれないのです。こうなっては困るので、このような定義は採用することはできません。

一般に、数学の世界で、あるものを表す方法が複数存在する場合（今のケースなら、整数を表す方法が複数ありますね）、それらを使って何かを定義したときに、どんな表し方をしても定義した内容が1つに定まる必要があります。表し方に関わらず内容が1つに決まる場合、代表元によらないといいます。

先ほどの「ダメな積」のように、何かを定義しても、その定義によって内容が定まらない場合もあるんですね。ちゃんと内容が決まる場合、つまり、代表元によらずに内容が決まる場合、この定義は well-defined であるといいます。この用語は、大学以降の数学でよく出てきます。「ちゃんと定義できている」という意味ですが、あまりいい日本語訳がないので、英語のまま使われることが多いです。

整数の加法が代表元によらずに決まることの確認

表し方が複数あるものに対して何かを定義する場合、表し方に関わらず内容が1つに決まる必要があるのでした。そのため、先ほどのように整数の加法を定義したい場合、他の表し方に対しても、和がきちんと1つの整数に定まるのか、確認する必要があります。この確認をして初めて、定義ができたことになります。

このような確認は今後何度も出てきます。基本的には、複数の表し方があったとして、同じ結果になるかどうかを確認するだけです。

今の場合であれば、 $[(a,b)]=[(a', b')]$, $[(c,d)]=[(c',d')]$ としたときに、どちらの表し方でも和が同じになるかを確かめることになります。つまり、\[ [(a+c,b+d)]=[(a'+c',b'+d')] \]が成り立つことを確かめればOKです。

$[(a,b)]=[(a', b')]$ であれば、 $a+b'=a'+b$ が成り立ちます。また、 $[(c,d)]=[(c', d')]$ であれば、 $c+d'=c'+d$ が成り立ちます。よって、辺々足すと $$\begin{aligned} (a+b')+(c+d') &= (a'+b)+(c'+d) \\[5pt] (a+c)+(b'+d') &= (a'+c')+(b+d) \\[5pt] \end{aligned}$$となります。これは、 $(a'+c',b'+d')\in [(a+c,b+d)]$ ということなので、たしかに、\[ [(a+c,b+d)]=[(a'+c',b'+d')] \]が成り立ちます。

つまり、他の表し方があったとしても、この定義を使えば、和は同じ整数を表すことになります。代表元によらずに、和を定めることができる、ということです。これで、先ほどの整数に対する加法の定義が well-defined であることが確かめられました。

整数の加法の定義

先ほどのチェックにより、次のように整数の加法の定義をします。

例えば、 $[(1,3)]+[(2,5)]$ は $[(3,8)]$ となります。これは、高校までの数学で見た表記に翻訳すれば、\[ (-2)+(-3)=(-5) \]ということです。今までの整数の加法と整合的であることがわかります。

なお、整数の加法の定義の中では、左辺の $+$ は、整数同士の加法のことで、「新しく定義するもの」です。一方、右辺にある2つの $+$ は、自然数同士の加法のことで、「すでに定義したもの」です。すでに知っているものを再構成する場合、「何を知っていて、何を定義しているのか」を意識しておかないと、何をやっているのかわからなくなってしまうので注意しましょう。

自然数の加法と整数の加法

自然数の整数への埋め込みでも見たように、自然数 $n$ と 整数 $[(n,0)]$ は同一視できるのでした。

これに従うと、2つの自然数 $a,b$ は、それぞれ $[(a,0)]$, $[(b,0)]$ と同一視できます。また、前者同士の和は $a+b$ であり、後者同士の和は $[(a+b,0)]$ です。つまり、和同士も対応することがわかります。

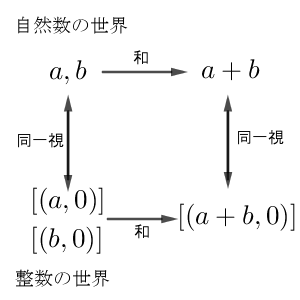
これは、元だけでなく、加法の構造も対応していると考えることができます。なので、整数の加法は、自然数の加法を拡張したものになっている、とも言えます。

おわりに

ここでは、整数の加法の定義を行いました。その際、和が代表元によらずに決まることを確認しました。このような確認は今後よく出てくることになります。

次は、整数の加法の性質をいくつか見ていくことにします。また、引き算の定義もようやく出てきます。