有理数の乗法の定義
有理数や加法の定義を行ったので、ここでは、有理数の乗法の定義を見ていきます。
有理数の乗法はどう定義するのが自然か?
有理数の加法の性質での冒頭でも見ましたが、まずは有理数に関するおさらいから始めます。
整数 $a\in\mathbb{Z}$ と $0$ 以外の整数 $b\in\mathbb{Z}^*$ を使って、ペア $(a,b)$ を考えます。このとき、 $[(a,b)]$ を次のように定義してグループ分けをしていきます。
$[(a,b)] = \lbrace (c,d)\mid ad=cb \rbrace$
これは、有理数を $\dfrac{a}{b}$ で表そうというアイデアに基づいています。 $ad=cb$ なら $a\div b=c\div d$ が成り立つのだから、同じ有理数を表すと考えて、同じグループに属するようにしています。こうして作られる $\lbrace [(a,b)] \rbrace$ を有理数の集合といい、各元を有理数と呼ぶのでした。
また、2つの有理数 $[(a,b)]$ と $[(c,d)]$ との和は、\[ [(ad+bc,bd)] \]で定義しました。これは、 $\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{ad+bc}{bd}$ というアイデアによります。こうすれば、代表元によらずに定義することができるのでした。
さて、加法を定義したので、次は乗法を定義してみましょう。これはどう定義するのがいいでしょうか。
高校までの内容を考えれば、有理数 $\dfrac{a}{b}$, $\dfrac{c}{d}$ の積は、 $\dfrac{ac}{bd}$ となります。これから考えると、 $[(a,b)]$ と $[(c,d)]$ との積は、 $[(ac,bd)]$ と定義するのが自然でしょう。
ところで、整数の和を定義するときに、「ダメな積」として「 $[(a,b)]$ と $[(c,d)]$ との積を、 $[(ac,bd)]$ と定義」することを見ました。有理数の乗法を定義しようとしている今の内容とまったく同じですね。
しかし、整数と有理数とでは、どのペアを同一視するかが違っています。そのため、整数のときにこの定義ではダメでも、有理数の場合にダメとは限りません。
以下では、このように有理数の積を定義するにあたって、代表元によって結果が変わらないことを見ていきます。
有理数の乗法が代表元によらずに決まることの確認
先ほどは、 $a,c\in\mathbb{Z}$, $b,d\in\mathbb{Z}^*$ として、有理数 $[(a,b)]$, $[(c,d)]$ の積は\[ [(ac, bd)] \]と定義するのが自然ではないか、という話をしました。このように定義するには、代表元によらずに値が決まることを確認しないといけません。有理数の表し方によらずに値が決まることをチェックしましょう。
$a', b', c', d'$ が、 $[(a,b)]=[(a',b')]$, $[(c,d)]=[(c',d')]$ を満たしているしましょう。つまり、同じ有理数に対して別の表し方をしてみる、ということです。このとき、もし先ほどのように積を決めたのであれば、 $[(ac, bd)]$ は $[(a'c', b'd')]$ に一致していないといけません。これを確認してみます。
$[(a,b)]=[(a',b')]$ なので、 $ab'=a'b$ が成り立ちます。同様に、 $cd'=c'd$ も成り立ちます。左辺同士、右辺同士を掛け合わせる(これは整数同士の掛け算です)と\[ (ab')\cdot(cd') = (a'b)\cdot (c'd) \]となります。整数の積の結合法則や交換法則を使って変形すれば、 $$\begin{aligned} (ac)\cdot(b'd') &= (a'c')\cdot(bd) \end{aligned}$$となるから、\[ [(ac,bd)]=[(a'c',b'd')] \]となることが示せました。
整数のときと有理数のときとでは、どのペアを同一視するかが異なっています。 $[(a,b)]$ と $[(c,d)]$ との積を $[(ac, bd)]$ と定義したとき、整数の場合は well-defined にはなりませんでした。同じ式で定義しても well-defined になったり、ならなかったりします。これは、どのペアを同一視するかという定義に戻って調べるしかありません。
有理数の乗法の定義
先ほどのチェックにより、代表元によらずに積を一つに決めることができることがわかったので、有理数の乗法を次のように定義します。
有理数の乗法
$a,c\in\mathbb{Z}$, $b,d\in\mathbb{Z}^*$ とする。このとき、有理数の乗法 $\cdot$ を次のように定める。 $$\begin{aligned} & [(a,b)]\cdot [(c,d)] \\[5pt] &= [(ac,bd)] \end{aligned}$$
なお、有理数の場合も、 $x\cdot y$ のことを $x\times y$ や $xy$ とも書きます。
例えば、 2つの有理数 $[(1,2)]$, $[(4,3)]$ の積は $$\begin{aligned} & [(1\cdot 4, 2\cdot 3)] \\[5pt] &= [(4,6)] \end{aligned}$$となります。 $4\cdot 3=2\cdot 6$ なので、これは $[(2,3)]$ とも同じです。小学校のときの計算でいえば、これは\[ \frac{1}{2}\times\frac{4}{3}=\frac{4}{6}=\frac{2}{3} \]という計算に対応します。
整数の乗法と有理数の乗法
有理数の定義でも見たように、整数 $z$ と 有理数 $[(z,1)]$ は同一視できるのでした。
これに従うと、2つの整数 $x,y$ は、それぞれ $[(x,1)]$, $[(y,1)]$ と同一視できます。また、前者同士の積は $xy$ であり、後者同士の積は $[(x\cdot y,1\cdot 1)]=[(xy,1)]$ です。つまり、積同士も対応することがわかります。
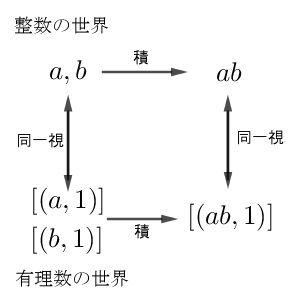
これは、元だけでなく、乗法の構造も対応していると考えられます。言い換えると、有理数の乗法は、整数の乗法を拡張したものになっている、とも言えます。
おわりに
ここでは、有理数の乗法の定義を行いました。今まで使っていた乗法と整合的になるように定め、その定義が well-defined であることも確かめました。
次は、この定義を使って、いろいろな有理数の乗法の性質を見ていきます。