自然数系の一意性
ここでは、自然数系が本質的に一意であることを見ていきます。
自然数系の作り方が複数あっても困らないのはなぜか
自然数の定義、自然数系の定義は、自然数の定義で行いました。振り返っておきましょう。
自然数の定義(ペアノの公理)
集合 $N$ は次を満たすとする。
- $0\in N$
- 各 $n\in N$ に対して、 $n^{+}\in N$ が1つ定まっている。
- $n\ne m$ ならば $n^{+}\ne m^{+}$ が成り立つ。
- $n^{+}=0$ となる $n\in N$ は存在しない。
- $N$ の部分集合 $S$ が次の(a)(b)を満たすなら、 $S=N$
(a) $0\in S$
(b) $s\in S$ ならば $s^{+}\in S$
このとき、 $N$ を自然数の集合といい、 $N$ の要素を自然数という。
そして、自然数の集合、最初の数、次の数を決める対応方法の3セットを自然数系と呼ぶのでした。つまり、自然数系とは、自然数たちをただ集めるだけではなく、各自然数の関係性・構造まで含めて考えますよ、ということです。
上の5つの条件を満たすものを、数学の言葉を使って作る方法も見ました(参考:自然数を構成するためのアイデア)。
1つ目の方法は、 $0$ と $\varnothing$ とを対応させ、 $n^{+}$ と $n\cup \lbrace n \rbrace$ とを対応させる、フォン・ノイマンの構成方法。
もう1つは、 $0$ と $\varnothing$ とを対応させ、 $n^{+}$ と $\lbrace n \rbrace$ とを対応させる、ツェルメロの構成方法です。
どちらの方法でも、上の性質を満たす自然数の集合が構成できています。公理の1と2はいいでしょう。4は、 $0$ が空集合に対応していることを考えれば、成り立つことがわかります。3は、集合の中身を考えるとわかります。5は、 $N$ に余分なものが入っていないので、これも成り立ちます。(ここのチェックを厳密にするには、「集合」をきちんと定義する必要がありますが、このシリーズでは省略しています)
ところが、この2つの構成方法を使ってできあがるものは、構造が違うようです。フォン・ノイマンの方法では $1\in 3$ なのに対し、ツェルメロの方法では $1\not\in 3$ です。構造が違っているのに、問題ないのでしょうか。
たしかに構造は違っています。しかし、それは自然数の性質と関係ない部分での違いです。なので、片方で $1\in 3$ で、もう片方で $1\not\in 3$ だからと言ってダメというわけではありません。
例えば、2つの三角形が相似かどうかを考えたい場合に、「辺の長さが違う」とか「面積が違う」といった違いはどうでもいいです。今注目したい性質と関係のない部分が違っていても、気にする必要はないんですね。
ただ、仮に、自然数系としての構造が違っていれば、それは問題です。気にしないといけないのは、自然数系の構造として同じなのかどうか、という点です。
自然数系の構造とは、最初の数があって、各数に対して次の数が1つ決まっている、という構造でした。これがそっくりそのまま互いにうつしあえるのであれば、それは構造として同じである、と言えるでしょう。
自然数系の一意性
では、自然数系の構造が同じである、というためには、何をいえばいいのでしょうか。
少なくとも、それぞれの値が1つ1つ対応する必要があります。ですが、それだけでは構造が同じとは言えません。自然数の集合とは、ただ要素が集まっているだけではなく、互いに関連しあっているからです。
例えば、「1,2,3」と「一,三,二」と対応させるのは、不自然でしょう。1つ1つ対応はしてますが、一の次に三が来るのはおかしいです。1の次に2が来るのだから、一の次に二が来るように対応させないとまずそうです。
このように、要素だけでなく、要素間の関係ごと対応していることが言えないと、構造が同じとは言えないでしょう。
ここで、2つの自然数系があったとしましょう。違いが分かるように、2つの自然数系を
- $(X, e_X, \varphi)$
- $(Y, e_Y, \psi)$
とします。つまり、前者の世界では、最初の数が $e_X$ で、 $x\in X$ の次の数は $\varphi(x)$ で表されます。後者の世界では、最初の数が $e_Y$ で、 $y\in Y$ の次の数は $\psi(y)$ で表される、ということです。
図で表すとこのような感じです。
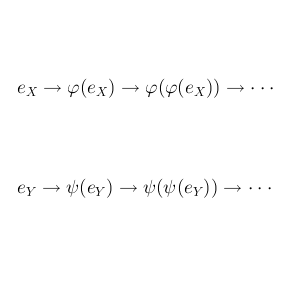
これらの構造が同じであるとは、「私の世界での『最初の数』は、あなたの世界での『最初の数』に対応していて、私の世界での『次の数の決め方』は、あなたの世界での『次の数の決め方』に対応している」ことが言えているときでしょう。そうすれば、世界を丸ごと変換することで、2つの世界を同一視できるはずです。
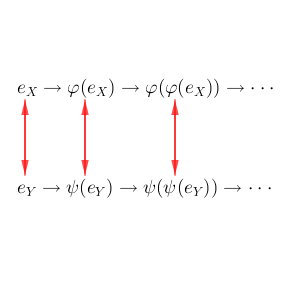
つまり、次を満たすような、 $X$ の各要素に $Y$ の各要素を1対1に対応させる関数 $f$ があればいいことがわかります。
- $f(e_X)=e_Y$
- $x\in X$ に対し、 $f(\varphi(x))=\psi(f(x))$
2つ目については、慣れていないと少しわかりづらいので、もう少し説明します。
$X$ の世界では $x$ の次が $\varphi(x)$ 、 $Y$ の世界では $y$ の次が $\psi(y)$ です。もし、2つの世界の構造が同じとすると、 $x,y$ が対応している場合は、次の数同士も対応している、つまり、 $\varphi(x)$ が $\psi(y)$ と対応しているべきです。これは\[ f(\varphi(x))=\psi(y) \]が成り立つということですが、 $y=f(x)$ なので、右辺は $\psi(f(x))$ と等しいです。これが 2つ目の条件の意味するところです。
イメージでいうと、次のような図になります。
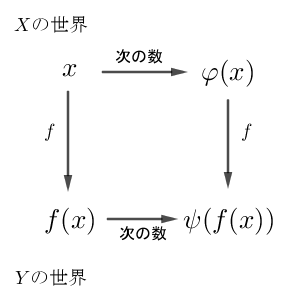
上の図では、左上から右下に移るのに、2つの経路があります。
- $x$ から下に行って右に行く( $Y$ の世界にうつしてから $Y$ の世界での次の数を考える)
- $x$ から右に行って下に行く( $X$ の世界での次の数を $Y$ の世界へうつす)
この2つの結果は、一般的に同じかどうかはわかりません。しかし、一致しているならば、 $X$ と $Y$ の要素が対応しているだけでなく、 $X$ 内の要素間の関係と $Y$ 内の要素間の関係が対応していることがわかります。世界を丸ごと変換できるので、構造が同じだと考えられます。
これらの条件を満たす関数は、最初の数から順番に対応させていくようにして作るのが自然でしょう。 $f$ を具体的に構成します。
まず、 $f(e_X)=e_Y$ とします。お互いの世界で、最初の数同士を対応させます。
次に、 $f(\varphi(e_X))$ には $\psi(f(e_X))$ を対応させます。先ほどの図で、 $x$ が最初の数のときに、下・右と移動しても、右・下と移動しても、結果が同じになるように定める、ということです。
以下、 $x\in X$ について、 $f(\varphi(x))$ に $\psi(f(x))$ を満たすように順番に定義していけば、関数 $f$ が定義できることになります。
このように順番に定義していくと、 $x\in X$ に対して $f(\varphi(x))$ の値が次々に決まるので、すべての $x\in X$ に対して値が定義できます。また、
$S=\lbrace y\in Y\mid f(x)=y$ を満たす $x$ が存在する $ \rbrace$
という集合を考えると、 $e_Y\in S$ であり、 $y\in S$ なら $\psi(y)\in S$ がわかります( $f(x)=y$ とすると、 $f(\varphi(x))=\psi(f(x))=\psi(y)$ だからです)。これより、 $S=Y$ であることがわかります。なので、 $Y$ の要素すべてが $f$ によって $X$ の何かの要素と対応されていることがわかります。
こうして、 $(X, e_X, \varphi)$, $(Y, e_Y, \psi)$ の構造を丸ごと対応付けできる関数 $f$ が作れるので、2つの世界は同一視することができます。つまり、今注目している自然数系の構造については、本質的な違いはない、ということです。
自然数系を複数作ったときに、自然数系の構造に関係のないところでは、構造に違いはあるかもしれません。でも、それは今は着目していないのだから、気にする必要はありません。
ここでは、関数 $f$ がどの値をどの値に対応させるか、次々に決めていく、というやり方を使いました。このようなやり方で定義することを、再帰的定義や帰納的定義といいます。
自然数が定義できることについて
今までの内容をまとめます。
まず、今までに学んだ自然数をもとにして、自然数の特徴をいくつか見てきました。それを用いて、自然数を定義しました。(参考:自然数の定義)
この性質を満たす自然数(自然数系)として、フォン・ノイマンの構築方法などを見ました。これにより、このような構造を持つものが1つは存在することがわかりました。(参考:自然数を構成するためのアイデア)。
そして、このページで見たように、このような構造が複数あっても、それらは構造的には同じであること、本質的に一意だということを見ました。
こうして、自然数の集合、自然数系の構造がうまく定義できたことになります。この自然数の集合を $\mathbb{N}$ で表します。そして、この集合の要素に、 $0,1,2,3,\cdots$ とラベルを付けて表すことにします。
なお、自然数の構成方法はいろいろありえますが、一般的には、フォン・ノイマンによる方法が採用されます。フォン・ノイマンによる方法では、 $1\in 3$ などが成り立ちますが、これが大小関係 $1\leqq 3$ とうまく対応できているように見えるから、などの理由があるためです。
自然数の構成関連のもっと細かい話
ここまでで、自然数を構成するという話はいったんおしまいです。ただし、専門書によっては、もっと細かなアプローチをとっていることもあります。
というのも、このサイトでの説明は、集合や関数(写像)について、特に説明せずに使ってきました。ここも本来はまじめにやる必要があります。
高校数学では、「モノの集まり」を集合と呼んでいました。このような定義で行う集合論のことを、素朴的集合論といいます。たいていのケースでは問題はなく、高校数学の範囲でも問題は起こらないのですが、ごくまれに致命的な問題が起きます。そのため、厳密に議論するなら、「こういうルールで作ったものだけを集合と認める」というルールを決めておく必要があります。
それに照らし合わせると、例えば、フォン・ノイマンによる構成で自然数を作った場合、ぜんぶ集めたものは(厳密な定義での)集合になるのか、といったことを気にする必要が出てきます。
また、自然数系の一意性を示すために、2つの自然数系を同一視するための関数を作りました。これも本当にちゃんと関数になっているか、つまり、「ある $x\in X$ に対しては、2つ以上の $y$ に対応するものしか作れない」みたいなことになっていないかを確認する必要があります。
「再帰的定義によって、無限回繰り返せばできます」と言っても、実際に無限回やることはできません。なので、本当にそれでうまく作れるかはわかりません。こうしたことをチェックするには、もっと基本的な内容をきちんと定義しないといけません。
このサイトではこれらの問題をスルーしていますが、集合や写像、論理などをきちんと定義して、より厳密に説明している専門書もあります。分野としては、「数学基礎論」と呼ばれています。このサイトとは議論の厳密さが異なりますが、「そういうところも気にしているんだな」というのがわかると、これらの専門書も読みやすくなるはずです。
おわりに
ここでは、自然数系の本質的な一意性について話をしてきました。構造として同一視できる、ということを見てきました。
今の時点では、まだ自然数(の構造)を定義しただけです。自然数同士の足し算、掛け算などはもちろん、大小関係すらもまだ定義はできていません。自然数の定義を新しくしたので、これらも新しく定義し直す必要があります。
次は、自然数の加法について考えていきます。その他の話題についても、今後、順番に見ていくことにします。