有理数の加法の定義

ここでは、有理数の加法を定義していきます。

有理数の加法はどう定義するのが自然か？

有理数の定義でも見ましたが、まずは簡単に有理数についておさらいしておきます。

整数 $a\in\mathbb{Z}$ と $0$ 以外の整数 $b\in\mathbb{Z}^*$ を使って、ペア $(a,b)$ を考えます。このとき、 $[(a,b)]$ を次のように定義してグループ分けをしていきます。

これは、有理数を $\dfrac{a}{b}$ で表そうというアイデアに基づいています。 $ad=cb$ なら $a\div b=c\div d$ が成り立つのだから、同じ有理数を表すと考えて、同じグループに属するようにしています。こうして作られる $\lbrace [(a,b)] \rbrace$ を有理数の集合といい、各元を有理数と呼ぶのでした。

例えば、 $(2,3)$ や $(4,6)$ や $(-200,-300)$ はいずれも同じグループ $[(2,3)]$ に属していて、そのグループは $\dfrac{2}{3}$ を表していると考える、というわけです。

---

このように有理数を定義した場合、有理数の加法はどう定義するのが自然でしょうか。

2つの有理数を、 $[(a,b)]$ と $[(c,d)]$ としましょう。これらは、心の中では $\dfrac{a}{b}$ と $\dfrac{c}{d}$ を表している、と考えます（が、分数を定義してないので、表舞台には出しません）。

こうしたとき、高校までの有理数の足し算を思い出せば、この2つの和は\[ \frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd} \]とするのが自然です。が、分数はまだ定義していないので、この書き方はまずいです。しかし、すでに定義した書き方を使えば、 $[(ad+bc,bd)]$ と表すことができます。なお、 $b\ne 0,d\ne 0$ なので、 $bd\ne 0$ となっています（参考：整数と簡約法則#整数の乗法と簡約法則の部分で、積が $0$ ならどちらかは $0$ であることを示しています）。

以上のことから、2つの有理数 $[(a,b)]$ と $[(c,d)]$ の和は、 $[(ad+bc,bd)]$ と定義するのが自然です。このように有理数の加法を定義すれば、高校までに扱ってきた有理数の加法と整合的になる、と考えられます。

有理数の加法が代表元によらずに決まることの確認

整数の加法のときには、加法を定義するときに「整数の表し方が1通りでない」ことが問題となっていました。有理数の加法でも同じ問題が起こります。

有理数の表し方は1通りではありません。そのため、先ほど述べたように有理数の和を定義したいと思っても、実際に定義できるかどうかはわかりません。先ほど述べたように有理数の和が定義できるかどうか、つまり、 well-defined であることをチェックしましょう。

$[(a,b)]=[(a',b')]$, $[(c,d)]=[(c',d')]$ とします。このとき、どちらの表し方でも和が同じになるかを確かめます。つまり、\[ [(ad+bc,bd)]=[(a'd'+b'c',b'd')] \]が成り立つことを確かめます。

$[(a,b)]=[(a',b')]$, $[(c,d)]=[(c',d')]$ から、 $ab'=a'b$, $cd'=c'd$ が成り立ちます。また、 $(ad+bc)b'd'$ と $(a'd'+b'c')bd$ をそれぞれ計算してみると、 $$\begin{aligned} & (ad+bc)b'd' \\[5pt] &= adb'd'+bcb'd' \\[5pt] &= ab'dd'+bb'cd' \\[5pt] \end{aligned}$$であり、 $$\begin{aligned} & (a'd'+b'c')bd \\[5pt] &= a'd'bd+b'c'bd \\[5pt] &= (a'b)dd'+bb'(c'd) \\[5pt] &= ab'dd'+bb'cd' \\[5pt] \end{aligned}$$となるので、等しいことがわかります。 $(ad+bc)b'd' = (a'd'+b'c')bd$ であることから、\[ (a'd'+b'c', b'd')\in [(ad+bc,bd)] \]が成り立ちます。よって、\[ [(ad+bc,bd)]=[(a'd'+b'c',b'd')] \]が成り立つことがわかります。

こうして、前述での有理数の和の定義は well-defined であることがわかります。

---

小学校のとき、有理数の足し算でよくある計算間違いに、分母同士、分子同士を足してしまう、つまり、 $\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{a+c}{b+d}$ としてしまうものがあります。

もしこう定義してしまうと、 $\dfrac{1}{4}+\dfrac{1}{2}$ と $\dfrac{1}{4}+\dfrac{4}{8}$ の答えが、それぞれ、 $\dfrac{2}{6}$ と $\dfrac{5}{12}$ となり、別の有理数を表すことになってしまいます。

有理数の表し方によって足した答えが変わってしまう、つまり、well-defined ではないことがわかります。そのため、そもそも定義することができません。

通分をして計算をする方法は、先ほど見たように well-defined です。分母同士、分子同士を足す間違いを笑う人がいるかもしれませんが、通分をして計算する方法が well-defined であることを確認していないなら、残念ながら笑う資格はないでしょう（確認してたとしても、人の間違いを笑うべきではないですが）。

小学校の時点で well-defined であることの確認まではやらないと思いますが、この確認をして初めて有理数の和がちゃんと定義できることがわかります。

有理数の加法の定義

先ほどのチェックにより、次のように有理数の加法の定義をします。

この式で、左辺にある "+" は有理数の加法であり、これから定義しようとしているものです。右辺にある "+" は、整数の加法であり、すでに定義したものです。同じ表記ですが、意味は異なります。

具体的な計算をしてみましょう。例えば、 $[(1,3)]+[(2,5)]$ は\[ [(1\cdot5+3\cdot 2,3\cdot 5)]=[(11,15)] \]となります。これは、高校までの数学で見た表記に翻訳すれば、\[ \frac{1}{3}+\frac{2}{5}=\frac{11}{15} \]ということです。今まで使ってきた有理数の加法と整合的であることがわかります。

整数の加法と有理数の加法

有理数の定義でも見たように、整数 $z$ と 有理数 $[(z,1)]$ は同一視できるのでした。

これに従うと、2つの整数 $x,y$ は、それぞれ $[(x,1)]$, $[(y,1)]$ と同一視できます。また、前者同士の和は $x+y$ であり、後者同士の和は $[(x\cdot1+y\cdot1, 1\cdot 1)]=[(x+y,1)]$ です。つまり、和同士も対応することがわかります。

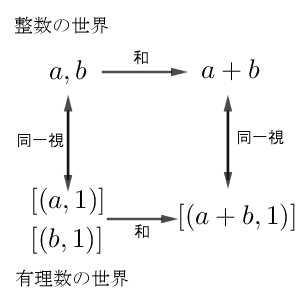
これは、元だけでなく、加法の構造も対応していると考えることができます。有理数の加法は、整数の加法を拡張したものになっている、とも言えます。

おわりに

ここでは、有理数の加法の定義を行いました。整数の加法のときと同様に、今まで使っていた加法と整合的になるように定め、その定義が well-defined であることも確かめました。

次は、この定義を使って、いろいろな有理数の加法の性質を見ていきます。