有理数の定義

ここまで、自然数や整数の定義をしてきたので、ここからは有理数の定義をしていきます。

有理数をどうやって定義するか

高校までの数学では、0以上の整数から始まり、次に有理数や小数、そして、整数という順番で学びます。一方、現代数学で数を構成する場合は、このサイトでも見てきた通り、自然数、整数の順番になることが多いです。そして、次が有理数(rational numbers) です。

自然数の世界では、加法と乗法が定義できました。また、整数の世界まで考えると、加法には常に逆元が存在するようになりました。しかし、乗法には逆元がつねにあるわけではありません。有理数は、乗法にも逆元が存在するように（いつでも割り算ができるように）導入します。

思い返してみると、整数を定義する際には、2つの自然数 $a,b$ を用いて $a-b$ と定義する、という発想を用いました（参考：整数の定義）。有理数を定義する際にも、この考え方が応用できそうです。

整数を定義したときには、まだ引き算を定義していなかったので、 $a-b$ ではなく、自然数のペアで考えました。有理数を定義する際にも、分数や比をいきなり導入するのではなく、すでに定義した数のペアで表すことにします。

もし割り算ができるようになれば、例えば、 $2\div 3$ は $\dfrac{2}{3}$ と書けます。

この右側を分数ではなく数のペアで表します。このとき、分子は整数なら何でもいいですが、分母は $0$ にできません。このことから、「 $0$ 以外の整数の集合」を定義しておいた方が便利そうです。この集合を $\mathbb{Z}^*$ と書くことにしましょう。

このとき、 $\mathbb{Z}$ と $\mathbb{Z}^*$ のペアで有理数を表すと考えます。

このようにペアで表すとすると、有理数が定義できているような気がします。

---

しかし、ここで整数のときと同じ問題が起こります。この表し方は1通りではありません。 $\dfrac{2}{3}$ と同じ数を表すペアは、他にも次のようなものがあります。

ここでも、やることはグルーピングです。同じ数を表していると考えるものは、同じグループにしてしまいます。

例えば、 $(2,3)$ と $(4,6)$ は同じ $\dfrac{2}{3}$ を表すことになってほしいです。こういうケースについて少し考えてみましょう。これは、割り算で考えると、次のように表せることに対応します。\[ 2\div 3=4\div 6 \]変形すると、次のようになります。\[ 2\cdot 6=4\cdot 3 \]$(2,3)$ と $(4,6)$ の外側同士、内側同士の積が等しいという式です。この両辺は、整数の乗法なので、本シリーズですでに定義しています。

これを踏まえると、次のように考えるのがいいでしょう。

整数のときと本当によく似た展開ですね。このように同じような流れの議論は、数学では抽象化してまとめて扱います。将来、集合論で「集合を同値関係で割る」ときに学ぶことになるでしょう。整数の定義の最後の部分に、ざっくりとした流れを書いています。

図で考えてみよう

有理数の定義についてさらに細かく見ていく前に、図でどういうことをやっているかを確認しておきましょう。

有理数1個を決めるために、 $a\in\mathbb{Z}$, $b\in\mathbb{Z}^*$ のペア $(a,b)$ を使うのだから、図では、2次元での点を考えることに対応します。

これらの点を全部使うことになったわけです。

ただ、 $ad=cb$ を満たすもの、分数で書けば $\dfrac{a}{b}=\dfrac{c}{d}$ を満たすものは、同一視するのでした。これは、各点と原点を結ぶ直線を次のようにかいた場合、同じ直線上にあるものはぜんぶ同一視する、と言うわけです。

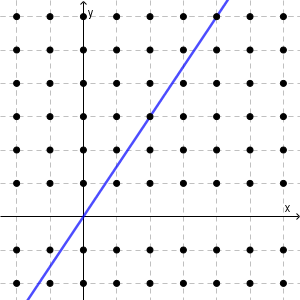
先ほど、 $(2,3)$ と $(4,6)$ が同じ整数を表すことを見ましたが、上の図では、この2点が同じ直線にあることに対応しています。

さらに言い換えると、それぞれの直線は、直線 $y=1$ 上の有理数の点に対応している、と考えることもできるでしょう。

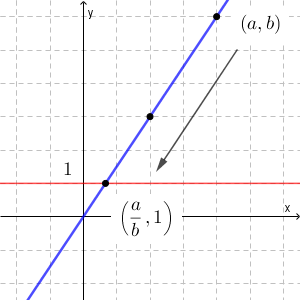
$(a,b)$ の各座標を $b$ で割れば、 $\left(\dfrac{a}{b}, 1\right)$ となります。このような対応だとわかれば、ペアを考えてグルーピング（同じ直線上にある点を同一視）したものを、有理数に対応させるのは、そんなに難しいことをやっているわけではないことがわかります。

直線 $y=0$ 上の点は、 $y=1$ と交わらないので、有理数の定義では使いません。 $0$ で割れないことは、この図ではこの2直線が交わらないことに対応している、と考えられます。

有理数はちゃんと定義できているか

さて、有理数の定義の話に戻りましょう。

$a\in\mathbb{Z}$, $b\in\mathbb{Z}^*$ のペア $(a,b)$ を使って、 $(a,b)$ で1つの有理数を対応させる、しかも、他のペア $(c,d)$ が $ad=cb$ を満たしていれば、 $(a,b)$ と $(c,d)$ は同じだとみなす。このように定義すればいいのではないか、という話でした。

こうすれば、 $(a,b)$ と等しいものを全部ひっくるめて、それら全部を $\dfrac{a}{b}$ のことだと思うようにすれば、たしかに有理数だと考えられるような気がします。先ほどの図でいえば、各直線に有理数を対応させていく、というイメージです。

しかし、ここでも、整数のときと同じように、well-defined であることを確かめないといけません。

$\mathbb{Z}, \mathbb{Z}^*$ のペアで、 $(a,b)$ と同じグループになるものを集めた集合を $[(a,b)]$ で表すことにします。つまり、\[ [(a,b)] = \lbrace (c,d) \mid ad=cb \rbrace \]ということです。わかりやすく言えば、 $\dfrac{a}{b}$ が同じ結果になるものをまとめたもの、ということですが、割り算を定義していないのでこういう書き方をしています。

このように定義するとき、整数のときと同様に、次の3つのことを確認する必要があるでしょう。

• $ad=cb$ のときに、 $[(a,b)]=[(c,d)]$ となること
• $(a,b)\in[(a,b)]$ となること
• $ad\ne cb$ のときに、 $[(a,b)], [(c,d)]$ の両方ともに属するものがないこと

1つ目が言えれば、同一視したいものは、ちゃんとグループとして同じになることがわかります。どのペアから出発しても、同じ集合が作られるということです。

2つ目が言えれば、モレているペアがないことがわかります。

3つ目が言えれば、同一視したくないものは別の集合になっていることがわかります。つまり、ダブっていないということです。

これらが言えれば、ペアをきれいに分割できていることが言えます。整数のときと似た流れですので、記憶があいまいな人は整数のときの話も見てみると参考になると思います。

---

これらを確かめていくのですが、確かめる際によく使う整数の乗法の簡約法則を見直しておきましょう。

まず、 $x,y\in \mathbb{Z}$ が $xy=0$ のとき、 $x=0$ または $y=0$ が成り立ちます。対偶である「 $x\ne 0$ かつ $y\ne 0$ ならば、 $xy\ne 0$ 」もよく使います。

また、 $z$ が $0$ でない整数のとき、 $xz=yz$ なら $y=z$ が成り立ちます。

これらを踏まえて、先ほどの内容を示していきます。

• $ad=cb$ のときに、 $[(a,b)]=[(c,d)]$ となること

$ad=cb$ とします。 $(e,f)\in[(a,b)]$ としたときに、 $(e,f)\in[(c,d)]$ となることを示しましょう。

$(e,f)\in[(a,b)]$ とすると、 $af=eb$ が成り立ちます。また、仮定より $ad=cb$ です。

もし $a=0$ なら、 $eb=0$, $cb=0$ です。 $b\ne 0$ だから乗法の簡約法則より、 $e=0$, $c=0$ です。なので、 $cf$, $ed$ はどちらも $0$ です。以上から\[ cf=ed \]が成り立ちます。

もし $a\ne 0$ なら、 $af=eb$ に $cb=ad$ を辺々掛けると\[ (af)\cdot (cb)=(eb)\cdot (ad) \]が成り立ちます。このとき、 $ab\ne 0$ なので、乗法の簡約法則や結合法則、交換法則から $ab$ を取り除いて\[ cf=ed \]が導けます。

どちらにしても $cf=ed$ が成り立ちます。これは $(e,f)\in[(c,d)]$ ということです。

逆も同じように示せます。これより、 $[(a,b)]$ と $[(c,d)]$ は、片方に属している元すべてがもう片方にも属していることがわかるので、集合として同じになります。

---

次にこれを確かめます。

• $(a,b)\in[(a,b)]$ となること

$(c,d)\in [(a,b)]$ は、 $ad=cb$ となることと同値です。 $c=a, d=b$ とすれば、この式は $ab=ab$ となりますが、これはもちろんいつでも成り立ちます。つまり、 $(a,b)\in[(a,b)]$ ということです。

---

最後にこれを確かめます。

• $ad\ne cb$ のときに、 $[(a,b)], [(c,d)]$ の両方ともに属するものがないこと

もし、 $(e,f)\in[(a,b)]$ と $(e,f)\in[(c,d)]$ が同時に成り立っていたとしましょう。このとき、 $af=eb$ と $cf=ed$ が成り立ちます。

$e=0$ とすると、 $af=0$, $cf=0$ で $f\ne 0$ だから $a=0$, $c=0$ となります。すると、 $ad=0$, $cb=0$ となり、 $ad\ne cb$ に矛盾します。

$e\ne 0$ とします。 $af=eb$ と $cf=ed$ に対し、2つ目の両辺を入れ替えて、1つ目の式に辺々掛けると\[ (af)\cdot(ed)=(eb)\cdot(cf) \]となります。が、 $ef\ne 0$ なので、 乗法の簡約法則を使って $ef$ を取り除くなどをすると\[ ad=cb \]となり、仮定と矛盾します。なので、 $(e,f)\in[(a,b)]$ と $(e,f)\in[(c,d)]$ は両方同時には成り立たないことがわかります。

有理数の定義

先ほどのチェックから、各 $[(a,b)]$ は、同じ有理数 $\dfrac{a}{b}$ を表すものたちで構成され、 $[(a,b)]$ たちを集めたものは、 $\mathbb{Z}, \mathbb{Z}^*$ のペアを、モレもダブりもなく分割できていることになります。この各 $[(a,b)]$ に $\dfrac{a}{b}$ を対応させる、と考えて、有理数は次のように定義します。

整数のときとかなり似た展開ですね。これが有理数の定義です。

有理数の一部を整数と同一視する

ここで、整数 $z$ と有理数 $[(z,1)]$ との関係を考えてみましょう。

整数 $z$ に 有理数 $[(z,1)]$ を対応させるのは簡単です。しかし、逆の対応は、少し注意が必要です。別の表し方があると困るからです。もし、 $[(z,1)]=[(w,1)]$ かつ $z\ne w$ だとしたら、「 $[(z,1)]$ には、 $z$ と $w$ のどちらの整数に対応させればいいか、決まらない」ことになってしまいます。

しかし、その心配はいりません。もし、 $(w,1)\in [(z,1)]$ だとすると、 $z\cdot 1=w\cdot 1$ が成り立ちます。これより、 $z=w$ となります。つまり、2つ目が $1$ になるように、 $[(z,1)]$ と表せば、 $z$ の値は1つに決まる、ということです。

このことから、整数 $z$ と 有理数 $[(z,1)]$ は1対1に対応します。そのため、この2つを同一視して考えることができます。

また、 $0$ ではない整数 $m$ を固定したとき、 $[(z,1)]$ と $[(zm,m)]$ は同じになります。それは、\[ z\cdot m=zm\cdot 1 \]からわかります。逆に、2つ目の数を $m$ と決めたとき、 $[(x,m)]$ が $[(z,1)]$ と等しくなるのは\[ x=zm \]のときだけです。このことから、 $[(zm,m)]$ も $z$ と同一視できます。

高校までの数学をもとに、2つの整数 $x,y$ $(y\ne 0)$ を使って、 $\dfrac{x}{y}$ で有理数を表すというアイデアを使っているので、 $z=\dfrac{z}{1}=\dfrac{zm}{m}$ から、整数 $z$ と 有理数 $[(z,1)]$ や有理数 $[(zm,m)]$ が対応することはそれほど違和感はないでしょう。

整数のときには、自然数は整数の一部と同一視できました。要素の対応だけでなく、足し算や掛け算の構造まで含めて対応していました。有理数も同様に、演算まで含めて、有理数の一部と整数とを対応付けることができます。今後、演算の定義と一緒に見ていきます。

おわりに

ここでは、有理数の定義を行いました。整数のときと同じように、きちんと定義できることを確認してから有理数の定義を行いました。

流れが整数のときと似ていますが、演算の定義なども整数のときと似ています。同じような考え方で理解していくことができます。