自然数の整数への埋め込み

ここでは、整数の定義を受けて、自然数を整数に埋め込む、ということをやっていきます。

整数の定義の振り返り

整数の定義はすでに行いましたが、同じ記号をこのページでも使うので、復習も込めて少し見直しておきましょう。

各整数は、2つの自然数 $a,b$ を使って、 $a-b$ で表すことにしよう、というアイデアを使いました。ただ、本シリーズではまだ引き算を定義していないので、 $(a,b)$ という自然数のペアで対応させることにしたのでした。

また、別の自然数 $c,d$ が、 $a+d=c+b$ を満たしているときは、（高校までの数学の知識を使うと） $a-c=b-d$ が成り立つので、 $(a,b)$ と $(c,d)$ は同じ整数を表している、と考えます。これに関連して、各 $(a,b)$ に対して、同じ整数を表している自然数のペアをグルーピングして集めたものを、次のように表します。\[ [(a,b)] = \lbrace (c,d) \mid a+d=c+b \rbrace \]このようにグルーピングしていくと、整数の定義で見たように、自然数のペアを、モレなくダブりなく分割できるのでした。そこで、グループ1つ1つに整数を対応させていく、と考えます。

こうして、例えば、 $[(1,3)]$ は、 $[(2,4)]$ や $[(10000,10002)]$ と同じものを表す、つまり、いずれも $-2$ を表していると考えるようにする、というわけです。

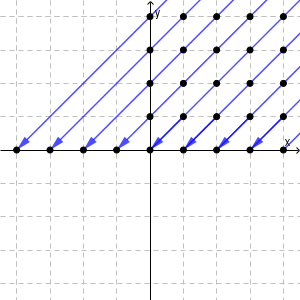
図を使えば、平面上で、座標がどちらも自然数の点を考え、直線 $y=x$ に平行な各直線の上にある点をすべて同一視することに対応しています。

これは、 $y=x$ にそって平行移動して $x$ 軸と交わった点を対応させていると考えることもできます。

整数の一部を自然数と同一視する

ここで、自然数 $n$ と 整数 $[(n,0)]$ との関係を考えてみましょう。

自然数 $n$ に 整数 $[(n,0)]$ を対応させるのは簡単です。しかし、逆の対応は、少し注意が必要です。別の表し方があると困るからです。つまり、もし、 $[(n,0)]=[(m,0)]$ かつ $n\ne m$ だとしたら、「 $[(n,0)]$ には、 $n$ と $m$ のどちらの自然数に対応させればいいか、決まらない」ことになってしまう、ということです。

しかし、その心配はいりません。もし、 $(m,0)\in [(n,0)]$ だとすると、定義から、 $n+0=m+0$ が成り立ちます。これより、 $n=m$ となります。つまり、2つ目が $0$ になるように $[(n,0)]$ と表せば、 $n$ の値は1つに決まる、ということです。

このことから、自然数 $n$ と 整数 $[(n,0)]$ は1対1に対応します。そのため、この2つを同一視して考えることができます。

そもそも、2つの自然数 $a,b$ を使って、 $a-b$ で整数を表すというアイデアを使っているので、 $n=n-0$ から、自然数 $n$ と 整数 $[(n,0)]$ が対応することはそれほど違和感はないでしょう。

正の整数

先ほどは、自然数 $n$ と 整数 $[(n,0)]$ が同一視できることを見ましたが、自然数のペアの2つ目の数が $0$ でない場合はどうなるかを考えてみましょう。

自然数 $a,b$ が $a\geqq b$ を満たすとします。このとき、 $a=b+n$ を満たす自然数 $n$ が存在します（参考：自然数の順序）。これを変形すると、 $n+b=a+0$ なので、 $(a,b)\in[(n,0)]$ だから、\[ [(n,0)]=[(a,b)] \]となります。このことから、 $[(a,b)]$ は $n$ と同一視できます。そのため、 $[(a,b)]$ を $n$ と表すことにします。

もう少し直接的に書くと、 $a=b+n$ ならば $[(a,b)]=[(b+n,b)]$ と書けますが、これは $[(n,0)]$ と一致するので、 $n$ と同一視できる、 $n$ と表す、ということです。

例えば、 $5=3+2$ なので、 $[(5,3)]$ は $2$ と表す、ということです。

自然数 $a,b,n$ が $a=b+n$ を満たすとき、 $n$ が $0$ でないときは $[(a,b)]$ を正の整数といいます。また、正の整数の集合を $\mathbb{Z}^{+}$ で表すことにします。 $n=0$ のときは、 $[(a,b)]=[(0,0)]$ であり、 $0$ と表します。

正の整数全体と $0$ を合わせたものは、自然数全体と1対1に対応できるため、自然数は整数の中に埋め込まれている、と考えることができます。現時点では、「元同士を1つ1つ対応させることが可能」という意味での対応を言っていますが、将来的には、加法や乗法の「構造」も込めて埋め込まれていることが確認できます。

負の整数

先ほどは、 $a\geqq b$ のときを見ましたが、2つの自然数 $a,b$ については、 $a\lt b$ のケースもあります（参考：自然数の順序）。

$a\lt b$ となることは、 $0$ でない自然数 $n$ を用いて $a+n=b$ と書けることと同値です。 $0+b=a+n$ なので、 $(a,b)\in[(0,n)]$ だから、\[ [(0,n)]=[(a,b)] \]となります。このように対応するときは、 $[(a,b)]$ を負の整数と言います。

また、負の整数の集合を $\mathbb{Z}^{-}$ で表すことにします。

もう少し直接的に書くと、 $a+n=b$ ならば $[(a,b)]=[(a,a+n)]$ と書けますが、これが $[(0,n)]$ になる、ということです。

将来的には、この場合、 $[(a,a+n)]$ には $-n$ を対応させるのですが、それはもう少し先で見ることにします。

整数の分類

自然数の順序でも見たように、自然数 $a,b$ に対しては、

のどれか1つだけが必ず成り立ちます。それぞれ、

と対応します。この $n$ を用いると、このページで見たように

と対応します。

$0$ でない自然数 $n$ について、 $[(n,0)]$ や $[(0,n)]$ が $[(0,0)]$ と等しくなることはありません。 $n+0\ne 0+0$ などからわかります。

また、 $[(n,0)]$ と $[(0,n)]$ と等しくなることもありません。 $n\ne 0$ のときは、 $n+n\ne 0+0$ となるからです。

つまり、整数は、正の整数、 $0$ 、負の整数という、重複のない3種類に分けられることがわかります。集合で表せば、\[ \mathbb{Z}=\mathbb{Z}^{+} \cup \lbrace 0 \rbrace\cup \mathbb{Z}^{-} \]が成り立つということです。右辺の集合には共通部分はありません。

はじめからもっとシンプルに定義できたのでは？という疑問について

ここまで来て、疑問に思う人がいるかもしれません。わざわざ自然数2つを使って $(a,b)$ と表して、それをグルーピングして $[(a,b)]$ を作って整数だと定義したのに、 $[(n,0)]$ や $[(0,n)]$ と同一視しました。それなら、最初から、 $(n,0)$ や $(0,n)$ を使うだけで良かったんじゃないか。こういう疑問です。

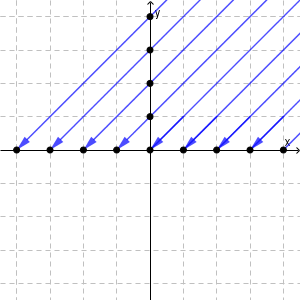
冒頭の図でいえば、もともとの定義では、自然数のペアを全部対象にして「直線上の点を同一視する」としていました。

こんなことをやらずに、 $x$ 軸と $y$ 軸にある点だけを考えればよかったんじゃないか、というわけですね。

最終的に同一視するなら、たしかにわざわざ $(a,b)$ 全体を考える必要がなかった、と感じるかもしれません。しかし、例えば、この次に見る整数の加法について考えると、わかりやすいかもしれません。

先に加法について書くと、 $[(a,b)]$ と $[(c,d)]$ の和は $[(a+c,b+d)]$ で定義しようと考えています（自然な決め方に見えますね）。この場合、例えば、 $[(1,0)]$ と $[(0,1)]$ の和は\[ [(1,1)] \]となります。これは、 $1$ と $-1$ の和が $0$ となることに対応しているのですが、「最初から $(n,0)$ や $(0,n)$ だけを使う」定義では、この $(1,1)$ をどう解釈すればいいか、困ってしまいます。

整数を定義するだけなら、「自然数のペア全体をグルーピングする」のは、手間がかかるだけのように見えますが、このように定義するほうがいいのは、先に進んでいくとわかるようになります。

大学以降の数学では、このように、「定義がやたらめんどうで、なぜこんな手間のかかることをやるのかわからない」という場面によく出くわします。しかし、この背景には、「後になると、実はいいことが起こる」「避けたい変な例がある」「他の分野でもよく使う手法を使い回している」などの理由があったりします。

なので、定義がよくわからない、しっくりこない、というときでも、ある程度読み進めていくことも大事です。また、先々まで行くと、なぜそう定義されたかが理解できるようになるかもしれないので、定期的に定義に戻ることも重要になります。

おわりに

ここでは、整数の一部が自然数と同一視できることや、整数が正の整数、 $0$ 、負の整数に分割できることなどを見ました。このように、世界を広げてから、「今まで考えていた世界が、新しい世界の一部になっている」ことを確認する作業は、数学の世界ではよく行います。この「数の構成」でもよく行っていくので、慣れていきましょう。