自然数の整列性と数学的帰納法
ここでは、自然数の整列性について説明し、数学的帰納法との関係について見ていきます。
最小元
自然数の順序で、自然数の順序を定義しました。このように、順序が定義された集合 $S$ があったときに、ある $m\in S$ があって
「 $s\in S$ ならば $m\leqq s$ 」
が成り立つとき、 $m$ を $S$ の最小元(least element) といいます。自然数全体の集合について考えると、最小元はもちろん $0$ です。
定理 (自然数の集合の最小元は0)
$x\in \mathbb{N}$ のとき、 $0\leqq x$ が成り立つ。
$0+x=x$ なので、順序の定義から $0\leqq x$ となることからわかります。これは、自然数の集合の最小元が $0$ であることを意味しています。
自然数の整列性
実は、全体だけではなく、任意の空でない部分集合についても最小元がある、というのが自然数の特徴です。このことを、整列性と呼びます。
定理 (自然数の整列性)
$S$ は $\mathbb{N}$ の部分集合で、 $S\ne\varnothing$ とする。このとき、 $S$ には最小元がある。
もしこの性質があれば、 $S$ の最小元がとれます。そして、その元を取り除いてまだ空集合でなければ、また最小元がとれます。これを繰り返していくと、 $S$ を小さい元から順番に並べていくことができる、整列できる、というわけです。
では、これを示してみましょう。
次のような集合 $T$ を考えます。
$T=\lbrace n\in \mathbb{N} \mid$ 任意の $s\in S$ に対して $n\leqq s$ $ \rbrace$
これは、イメージでいうと、最小元の候補の集合です。この中に $S$ にも属しているものがあれば、それが最小元です。
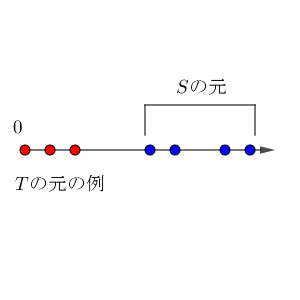
上のイメージ図からもわかりますが、 $S$ の一番左にある元が $S$ の最小元になると予想できます。そして、これは $T$ の最大元にもなっています。これを利用することを意識して、示します。
証明の流れとしては、まず、 $T$ に最大元があることを示します(最大元がなければ、$T$ は自然数全体となって矛盾する、という手法を使います)。次に、この最大元が $S$ に属していなければ、矛盾することをいいます。これは、もし $S$ に属していないなら、 $T$ の最大元の次の数も $T$ に属してしまう、という手法を使います。こうして、 $T$ の最大元が $S$ の最小元でもあることを示します。
さて、まず、先ほど示した通り、自然数の集合の最小限は $0$ なので、どんな $s\in S$ に対しても $0\leqq s$ となるから、 $0\in T$ です。
次に、 $S$ に属する、ある $s$ をとってきます。このとき、 $s\lt s+1$ が成り立ちます。つまり、 $s+1$ は $s$ 以下ではないので、 $s+1\not\in T$ となります。これから、 $T\ne \mathbb{N}$ となるので、
(*) $m\in T$ かつ $m+1\not\in T$
となる $m\in \mathbb{N}$ が存在します(もしすべての $m$ に対して「 $m\in T$ ならば $m+1\in T$ 」が成り立つなら、数学的帰納法の原理から $T$ は $\mathbb{N}$ に一致してしまうため)。
$m\in T$ なので、
「任意の $x\in S$ に対して $m\leqq x$ 」
が成り立ちます。
以下では、もし $m\not\in S$ なら、矛盾することを示します。 $m\not\in S$ なら、 $m\leqq x$ の等号が成り立つことはないので、
「任意の $x\in S$ に対して $m\lt x$ 」
となります。
これより、 $0$ でない自然数 $a$ があって、\[ m+a=x \]とかけます。 $a$ が $0$ でないときは、 $w^{+}=a$ となる自然数 $w$ が存在する(参考:自然数の定義#自然数の性質の後半)ので、
$$\begin{aligned}
m+w^{+} &= x \\[5pt]
m+(w+1) &= x \\[5pt]
m+(1+w) &= x \\[5pt]
(m+1)+w &= x \\[5pt]
\end{aligned}$$となるから、順序の定義より
「任意の $x\in S$ に対して $m+1\leqq x$ 」
が成り立ちます。これは $m+1\in T$ ということなので、(*)に矛盾します。
$m\not\in S$ とすると矛盾することから、 $m\in S$ であり、
「任意の $x\in S$ に対して $m\leqq x$ 」
が成り立つから、 $S$ には最小元 $m$ があることがわかります。
自然数の場合は整列性がありますが、有理数や実数の場合などはこうはなりません。例えば、正の有理数の集合、正の実数の集合には、最小元はありません。最小元はその集合に属していないといけないので、これらのケースでは $0$ は最小元とはなりません。
自然数の整列性と数学的帰納法の原理
先ほどの証明を見直してみましょう。
$T=\lbrace n\in \mathbb{N} \mid$ 任意の $s\in S$ に対して $n\leqq s$ $ \rbrace$
という集合を考えた場合、 $0\in T$ が成り立ちます。また、もし、すべての $m\in T$ について
$m\in T$ ならば $m+1\in T$
が成り立つなら、数学的帰納法の原理により $T=\mathbb{N}$ となりますが、 $T$ に属さない元がある(例えば、 $S$ の元より大きい元など)ので、これは成り立ちません。そのため、
$m\in T$ かつ $m+1\not\in T$
となる $m$ が存在し、結局、これが $S$ の最小元となるのでした。
この証明から、自然数の整列性は、数学的帰納法の原理から導き出されていることがわかります。ところが、実は、この逆も導けるのです。
定理 (自然数の整列性から数学的帰納法の原理)
$\mathbb{N}$ の、空でない部分集合には、必ず最小元があるとする。
このとき、 $\mathbb{N}$ の部分集合 $S$ が次の(a)(b)を満たすなら、 $S=\mathbb{N}$ が成り立つ。
(a) $0\in S$
(b) $s\in S$ ならば $s^{+}\in S$
厳密にやるなら、自然数やその順序などを、数学的帰納法の原理を使わずに整列性から定義していく必要があります(当サイトでは、数学的帰納法の原理を自然数の定義の中に入れているからです)。ただ、それをやりだすとまたすごく長くなるので、ここではそれらが定義できたとして示すことにします。なので、以下の内容は証明というよりは、証明の概要のようなものです。
$S$ の補集合 $S^c$ を考えます。つまり、
$S^c=\lbrace n\in \mathbb{N} \mid$ $n\not\in S$ $ \rbrace$
です。このとき、 $S^c=\varnothing$ なら、 $S=\mathbb{N}$ が言えます。
もし、 $S^c$ が空集合でないとすると、自然数の整列性から、最小元 $m$ が存在します。特に、 $m\in S^c$ が成り立つことに注意しましょう。
さて、(a)より、 $0$ は $S^c$ に属さないので、 $m\ne 0$ です。このとき、 $w^{+}=m$ となる $w$ が存在します。 $w\lt m$ なので、 $m$ の最小性から $w\not\in S^c$ が成り立ちます。つまり $w\in S$ となります。
(b)より $w^{+}\in S$ となりますが、これは $m\in S$ のことであり、 $m\in S^c$ であることに矛盾します。
以上から、 $S^c=\varnothing$ なので、 $S=\mathbb{N}$ が示せました。
これより、数学的帰納法の原理と整列性は同値だとわかります。そのため、自然数の定義を行うときには、数学的帰納法の原理ではなく、整列性から出発して考えていく方法(や専門書)もあります。
ただ、数学的帰納法の原理のほうが使い勝手がいいことや、ペアノが発表した内容には数学的帰納法の原理が採用されていたことなどから、数学的帰納法の原理の方を出発点とすることが多いです。
いろいろな数学的帰納法の形
ついでに、数学的帰納法の話をいろいろしておきましょう。
ペアノの公理の5つ目のことを数学的帰納法の原理といいます。次のような内容です。
定理 (数学的帰納法の原理)
$\mathbb{N}$ の部分集合 $S$ が次の(a)(b)を満たすなら、 $S=\mathbb{N}$
(a) $0\in S$
(b) $s\in S$ ならば $s^{+}\in S$
加法を定義した今となっては、 $s^{+}$ を $s+1$ に書き換えても構いません。
これを命題の形に言い換えた、数学的帰納法もよく使います。
定理 (数学的帰納法)
自然数 $n$ に関する命題 $P(n)$ が次の(a)(b)を満たすなら、すべての自然数 $n$ について $P(n)$ が成り立つ。
(a) $P(0)$ が成り立つ。
(b) $P(k)$ が成り立つならば $P(k+1)$ が成り立つ。
これは、
$S=\lbrace k\in \mathbb{N} \mid P(k)$ が成り立つ $ \rbrace$
という部分集合を考えれば簡単に示せます。逆に、数学的帰納法の原理を示すには、
$P(n):$ $n\in S$
という命題を考えれば示せます。つまり、集合の形で書いても、命題の形で書いても、実質同じことというわけです。
数学的帰納法に似た次の形を使って証明を行うこともあります。過去のすべての結果を使うので、累積帰納法といいます。
定理 (累積帰納法)
自然数 $n$ に関する命題 $P(n)$ が次の(a)(b)を満たすなら、すべての自然数 $n$ について $P(n)$ が成り立つ。
(a) $P(0)$ が成り立つ。
(b) $k$ 以下のすべての $m\in \mathbb{N}$ について $P(m)$ が成り立つならば、 $P(k+1)$ が成り立つ。
数学的帰納法が成り立てば、累積帰納法も成り立ちます。これをまず示してみます。数学的帰納法から自然数の整列性が示せるので、それを使って示します。
累積帰納法の仮定が成り立つとして、集合 $S$ を次のように定義します。
$S=\lbrace n\in\mathbb{N}\mid$ $P(n)$ が成り立たない $ \rbrace$
ここで、もし $S$ が空集合でないとすると、自然数の整列性から、 $S$ には最小元 $m$ が存在します。(a)より $P(0)$ が成り立つので、 $m\ne 0$ だから、 $m=w^{+}$ を満たす $w\in\mathbb{N}$ が存在します。
このとき、最小性から、 $0\leqq k\leqq w$ を満たすすべての $k\in \mathbb{N}$ について、 $P(k)$ が成り立ちます。(b)より $P(w^{+})$ が成り立ちます。つまり、 $P(m)$ が成り立ちますが、これは $m\in S$ に矛盾します。
これから、 $S$ は空集合であり、すべての自然数 $n$ について $P(n)$ が成り立つこと、つまり、累積帰納法が成り立つことがわかります。
この逆も成り立ちます。つまり、累積帰納法から数学的帰納法を導けます。これも示してみましょう。
自然数 $n$ に関する命題 $P(n)$ が次の(a)(b)を満たすとします。
(a) $P(0)$ が成り立つ。
(b) $P(k)$ が成り立つならば $P(k+1)$ が成り立つ。
数学的帰納法の仮定が成り立つ、とするわけですね。
このとき、累積帰納法に出てくる
$k$ 以下のすべての $m\in \mathbb{N}$ について $P(m)$ が成り立つ
について考えてみましょう。 $k$ 以下で成り立つなら、 $m=k$ のときも成り立ちます。つまり、 $P(k)$ が成り立つということです。このことから、(b)より $P(k+1)$ が成り立ちます。つまり、累積帰納法の(b)が成り立つということです。
これと $P(0)$ が成り立つことから、累積帰納法が使えるので、すべての自然数 $n$ について $P(n)$ が成り立つことがわかります。
こうして、累積帰納法から数学的帰納法が導けました。先ほどの内容と合わせると、次の3つは互いに同値であることがわかります。
数学的帰納法に同値なもの
- 数学的帰納法
- 累積帰納法
- 整列性
おわりに
ここでは、自然数の整列性と数学的帰納法、累積帰納法について紹介し、これらが互いに同値であることを見てきました。
数学的帰納法は今後もよく使います。集合の形ではなく、命題の形で書いたものも今後は使っていきます。